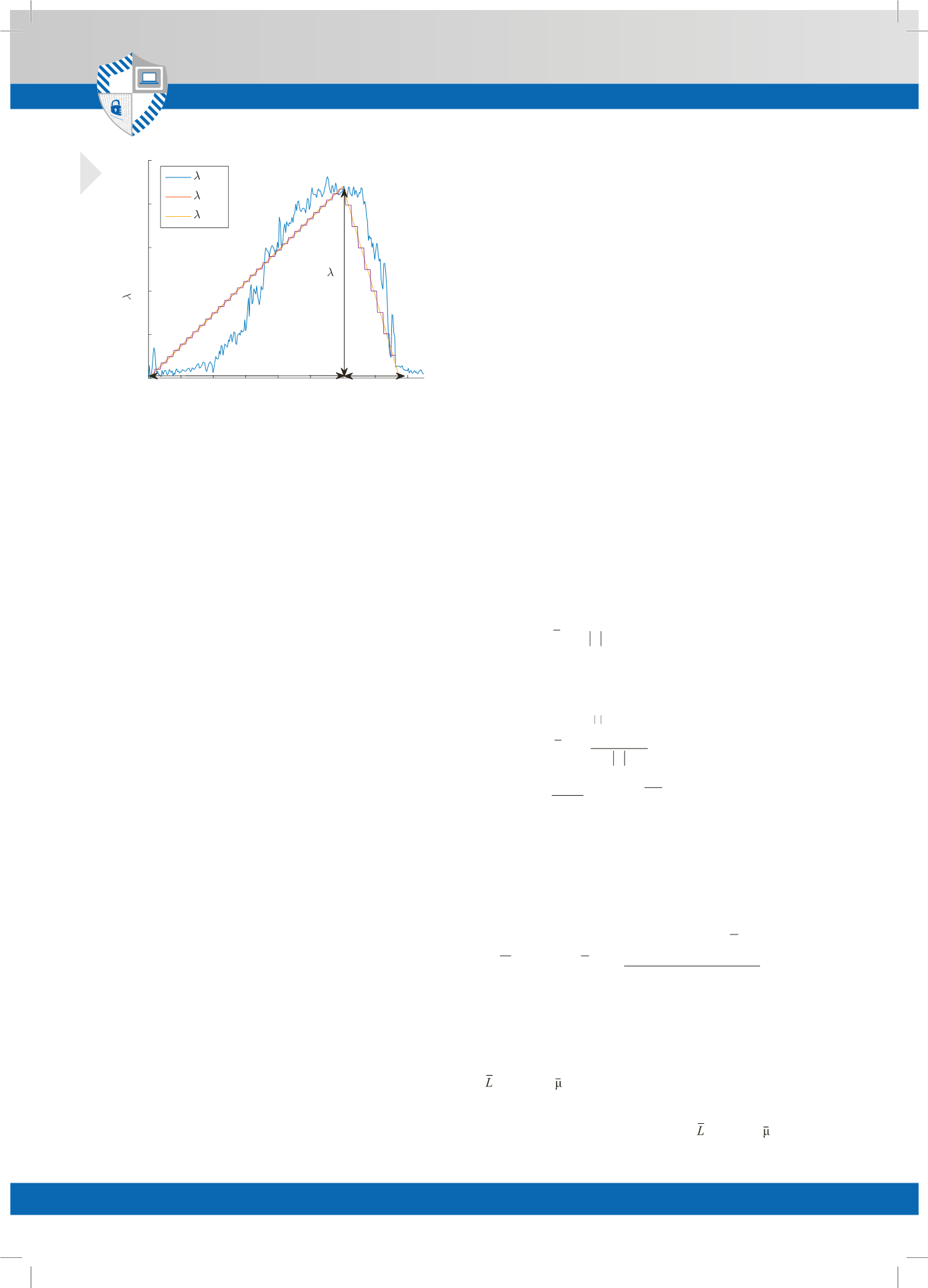
Выбор зависимости был основан на результатах ста-
тистического анализа реальных данных, проведенного
в [4]. Типичная зависимость
λ
exp
(
t
)
, полученная во время
проведения футбольного матча между футбольными клу-
бами «Урал» и «Анжи» на Центральном стадионе (ЦС)
г. Екатеринбурга 27.09.2012, приведена на рисунке 2.
Из рисунка 2 видно, что доступ на ЦС был открыт за
2 ч. до начала футбольного матча. В рассматриваемой
НСМО после открытия турникетов в течение времени
T
1
=120 мин интенсивность поступления заявок нарас-
тала от 0 чел/мин до
λ
max
=22 чел/мин. После начала
матча в течение временного интервала
T
2
=30 мин.
интенсивность уменьшилась от
λ
max
=22 чел/мин до
0 чел/мин. Таким образом, общее число вошедших на
ЦС через один турникет составило 1700 чел.
При моделировании был использован кусочно-
линейный закон
λ
=
λ(
t
)
. На временном интервале
T
1
[-120;0] минут
λ(
t
)
возрастала по линейному закону от
0 до
λ
max
, далее на временном интервале
T
2
[0;30] минут
линейно убывала от
λ
max
до 0. При этом
λ
max
выбиралось
таким образом, что общее число вошедших составляло
1700 чел. При проведении статистических испытаний
для выбранного закона
λ
schem
(
t
)
использовалась кусоч-
но-постоянная аппроксимация (рис. 2).
При этом длительность интервала аппроксимации
выбиралась, следуя [3], равной 30 с, а значение интен-
сивности на соответствующем интервале — среднему
значению интенсивности на данном интервале.
3. МЕТОДИКА ПРОВЕДЕНИЯ
ВЫЧИСЛИТЕЛЬНЫХ ЭКСПЕРИМЕНТОВ
Блок-схема алгоритма, использовавшегося при про-
ведении статистического моделирования, подробно
описана в [3]. На каждом из интервалов кусочно-посто-
янной аппроксимации в течение интервала генериро-
вались времена прибытия заявки
t
A
с экспоненциаль-
ным законом распределения и интенсивностью равной
усредненному значению интенсивности прибытия.
Интервал времени обслуживания генерировался со-
гласно формуле (1). Далее для заявок производился
расчет времени постановки на обслуживание
τ
S
путем
поочередного просмотра всех заявки, стоявших на
данном интервале очереди на обслуживание:
Отметим, что, как очевидно, для первой заявки
t
E1
=
t
A1
.
В ходе проведенных испытаний параметры
T
1
,
λ
max
при
фиксированном параметре
T
2
=30 мин. варьировались
таким образом, что общее число заявок
N
(посетите-
лей) оставалось равным 1700. В связи с тем, что при
фиксированных
N
и
T
2
значения параметров
T
1
,
λ
max
оказываются линейно зависящими друг от друга:
λ
max
=2 .
N
/(
T
1
+
T
2
), (4)
достаточно варьировать один из параметров, например,
T
1
.
Параметр
T
1
варьировался в диапазоне
•
-310,-87
–
мин.,
соответственно, значение
λ
max
варьировалось в диа-
пазоне
•
10,29
–
чел/мин. Анализ характеристик, ис-
пользуемых для описания особенностей работы
данных НСМО [3], показал, что для их количественного
описания можно, например, использовать зависимость
длины очереди посетителей (в терминах СМО — длины
очереди заявок) от времени:
А также среднее время ожидания посетителя (в тер-
минах СМО заявки) в очереди от времени:
где
K
—количество интервалов кусочно-линейной аппрок-
симации
λ(
t
)
.
Так как при моделировании использовался метод
Монте-Карло, в качестве значений функции характери-
стик нестационарной СМО принимались их средние по
ансамблю независимых реализаций значения:
где
m
— число независимых испытаний в методе Мон-
те-Карло,
Ф
— элемент множества
{
L,τ
w
}
.
4. АНАЛИЗ ЭКСПЕРИМЕНТАЛЬНЫХ РЕЗУЛЬТАТОВ
Рассмотрим результаты расчетов функции
(
T
1
,
T
2
,
λ
max
, ,
t
k
)
, в которых число интервалов ку-
сочно-линейной аппроксимации зависимости
λ(
t
)
K
равнялось 680, число независимых статистических
испытаний
m
— 1000. Зависимости
(
T
1
,
T
2
,
λ
max
, ,
t
k
)
t
, мин.
-120
-100
-80
-60
-40
-20
0
20
40
, чел./мин.
0
5
10
15
20
25
T
1
T
2
A
B
C
max
exp
schem
model
Рисунок 2.
Зависимости
λ(
t
)
нестационарной СМО (начало матча
t
=0)
( )
30
120
N
t dt
−
= λ
∫
(2)
1
1
1
1
1
1
,при
(
),при
i
i
i
i
i
i
i
i
i
i
i
i
A
A E
S
E
A
E
S
A
A E
S
t
t
t
t
t
t
t
t
t
−
−
−
−
−
−
> + τ
= + + τ −
> + τ
(3)
(
)
, ,
,где { :
}
n
n
max
k
n A k
E k
L L
t
Q Q q t
t
t
t
= λ µ =
=
< ∩ >
(5)
(
)
(
)
1 2
1
1 2
, ,
, ,
, ,
, ,
,
m
j
max
k
j
max
k
T T
t
T T
t
m
=
Φ λ µ
Φ λ µ =
∑
(7)
(
)
1
1
(
)
, ,
,где { :
}
i
i
n
n
Q
E A
i
w w max
k
n E k
E k
t
t
t
Q q t
t
t
t
Q
=
−
−
τ = τ λ µ =
=
≤ ∩ >
∑
(6)
(
)
2 1
1
1 ,
k
T T
t
T
k
K
−
= +
−
1, ,
k K
=
56
СБОРНИК ДОКЛАДОВ
МЕЖВЕДОМСТВЕННАЯ НАУЧНО-ПРАКТИЧЕСКАЯ КОНФЕРЕНЦИЯ
СПЕЦИАЛЬНЫЕ ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
2017


