для
λ
max
Ý•
10,29
–
чел/мин,
T
1
Ý•
-310,-87
–
мин,
T
2
=30 мин,
Ý•
10;12;15;20
–
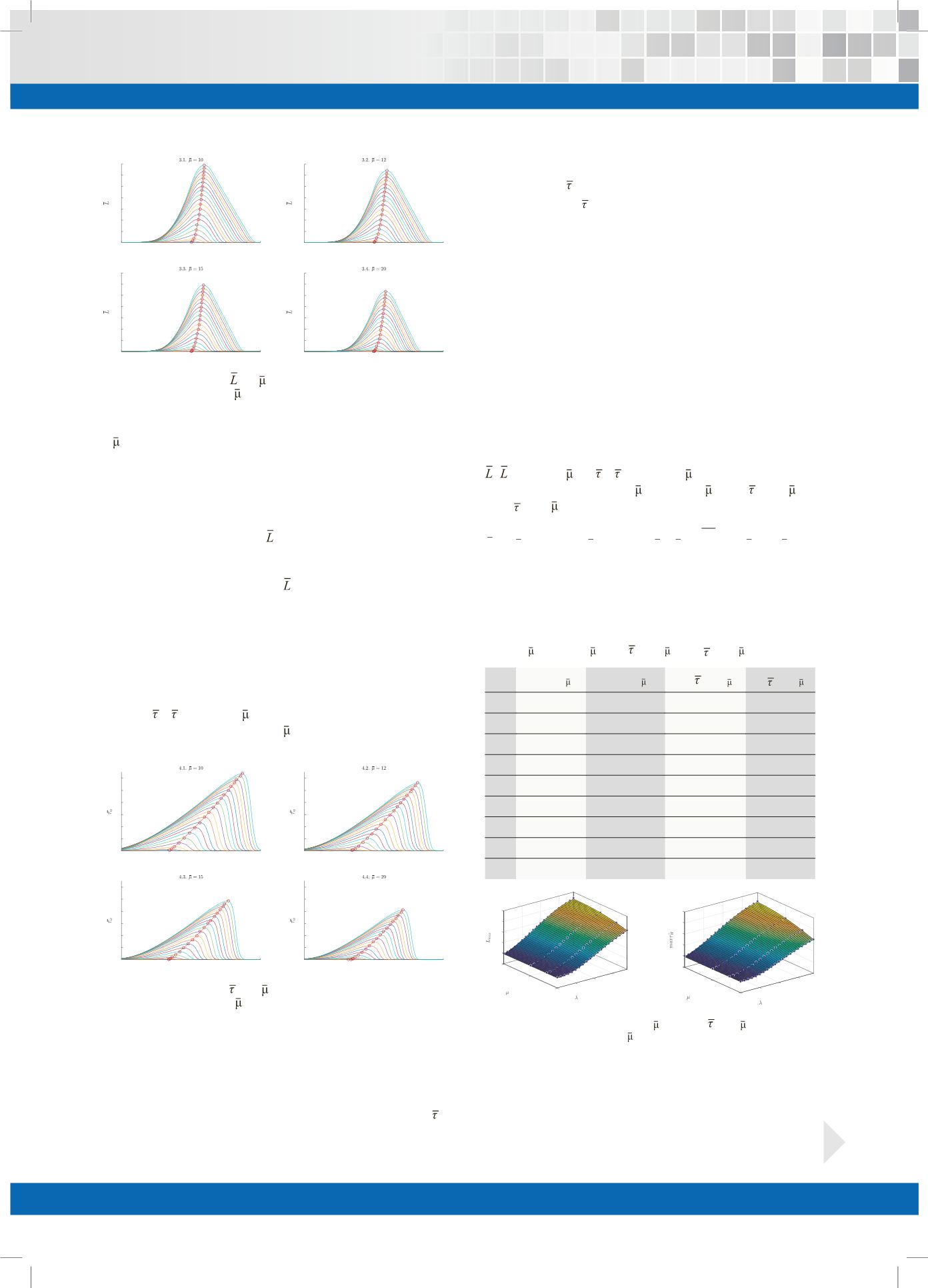
чел/мин представлены на рис. 3.
Из рисунка 3 видно:
•
в выбранном диапазоне значений параметров
НСМО средняя длина очереди монотонно возраста-
ет до максимального значения, после чего моно-
тонно убывает;
•
максимальная длина
max
очереди зависит от про-
изводительности устройства обслуживания;
•
значение времени
t
Lmax
, соответствующего макси-
мальной длине очереди
max
, зависит от произво-
дительности обслуживающего устройства;
•
длина очереди, после прекращения поступления
заявок в очередь, линейно убывает, при этом
скорость убывания зависит от обслуживающего
устройства.
Также были вычислены зависимости време-
ни ожидания в очереди от времени и параметров
НСМО
w
=
w
(
T
1
,
T
2
,
λ
max
, ,
t
k
)
для
λ
max
Ý•
10,29
–
чел/мин,
T
1
Ý•
-310,-87
–
мин,
T
2
=30мин,
Ý™
10;12;15;20
š
чел/мин,
представленные на рис. 4.
Из рисунка 4 видно:
•
в выбранном диапазоне значений параметров
системы среднее время ожидания в очереди моно-
тонно возрастает до некоторого максимального
значения, после чего монотонно убывает;
•
что максимальное время ожидания в очереди
max
w
зависит от интенсивности поступления заявок
и производительности устройства обслуживания;
•
значение максимального времени ожидания в оче-
реди
max
w
достигается в различные моменты
времени
t
max w
, зависящем от интенсивности посту-
пления заявок и производительности устройства
обслуживания.
Отметим, что представленные результаты модели-
рования НСМО согласуются с физическими представ-
лениями. Действительно, увеличение интенсивности
поступления заявок при фиксированном времени их
обслуживания должно приводить к увеличению длины
очереди и, соответственно, увеличению времени
обслуживания заявок, находящихся в очереди после
окончания их поступления. И, наоборот, уменьшение
времени обслуживания заявок при фиксированной
интенсивности их поступления приводит к уменьшению
длины очереди и, соответственно уменьшению вре-
мени обслуживания заявок, находящихся в очереди,
после окончания их поступления.
Анализ зависимостей
=
(
T
1
,
T
2
,
λ
max
, ,
t
k
)
,
w
=
w
(
T
1
,
T
2
,
λ
max
, ,
t
k
)
, показывает,
что зависимости
L
max
(λ
max
,
)
,
t
L max
(λ
max
,
)
,
max
w
(λ
max
,
)
и
t
max
w
(λ
max
,
)
могут быть аппроксимированы функцией
от двух переменных вида:
где значения коэффициентов
a
i
,
i
=0,8 вычисленные
в соответствие с методом наименьших квадратов,
представлены в таблице 1. А аппроксимирующие по-
верхности показаны на рисунке 5.
Таким образом, полученные моделирования НСМО
результаты, согласующиеся с физическими пред-
ставлениями об особенностях ее функционирования,
подтверждают адекватность использованной матема-
тической модели НСМО и работоспособность соответ-
ствующей программной реализации.
t,мин.
-100
-50
0
50
100
0
100
200
300
400
500
600
700
t,мин.
-100
-50
0
50
100
0
100
200
300
400
500
600
700
t,мин.
-100
-50
0
50
100
0
100
200
300
400
500
600
700
t,мин.
-100
-50
0
50
100
0
100
200
300
400
500
600
700
t,мин.
-50
0
50
100
0
10
20
30
40
50
60
t,мин.
-50
0
50
100
0
10
20
30
40
50
60
t,мин.
-50
0
50
100
0
10
20
30
40
50
60
t,мин.
-50
0
50
100
0
10
20
30
40
50
60
Рисунок 3.
Зависимости
(λ
max
, ,
t
)
(начало матча
t
=0) для различных
значений параметров
λ
max
,
Таблица 1.
Значения коэффициентов функциональных зависимостей
L
max
(λ
max
,
)
,
t
L max
(λ
max
,
)
,
max
w
(λ
max
,
)
и
t
max w
(λ
max
,
)
Рисунок 5.
Зависимости (a)
L
max
(λ
max
,
)
и
(б)
max
w
(λ
max
,
)
для различ-
ных значений параметров
λ
max
,
Рисунок 4.
Зависимости
w
(λ
max
, ,
t
)
(начало матча
t
=0) для различных
значений параметров
λ
max
,
(
)
2
2
3
2
2
max
0
1
2
5
4
3
6
7
8
,
max
max
max
max
max
max
F
a a
a a
a
a a
a
a
λ µ = + λ + µ + λ + λ µ + µ + λ + λ µ + λ µ
,
(8)
25
max
,чел/мин.
20
15
10
10
,чел/мин.
15
-200
0
200
400
800
600
20
25
max
,чел/мин.
20
15
10
10
,чел/мин.
15
-20
0
20
40
80
60
20
(a)
(б)
L
max
(λ
max
,
)
t
L max
(λ
max
,
)
max
w
(λ
max
,
)
t
max w
(λ
max
,
)
a
0
970±160
-32±(-3,3)
99±13
-72±12
a
1
-167±16
2,4±0,18
15,5±1,3
3,4±0,7
a
2
-54±17
1,1±0,37
-6,4±1,4
3,3±1,3
a
3
7,8±0,7
-0,04±(-0,01)
0,66±0,06 -0,025±0,015
a
4
7±1
0,004±(-0,005)
0,7±0,08
0,1±0,021
a
5
0,66±0,54 -0,025±(-0,011)
0,099±0,045 -0,12±0,04
a
6
-0,1±0,11
0
-0,0092±0,0009
0
a
7
-0,09±0,015
0
-0,0075±0,0012
0
a
8
-0,078±0,027
0
-0,0095±0,0022
0
57


