тителей футбольных матчей на стадион
λ
(t). Каждая из
зависимостей
λ
(t) на временном интервале [T
1
, T
2
] (Т
1
—
момент времени, соответствующий открытию доступа
на стадион, Т
2
— момент времени, соответствующий
входу на стадион последнего посетителя) представляет
собой сумму некоторой детерминированной
λ
det
(t) и слу-
чайной
λ
rnd
(t):
λ
(t)=
λ
det
(t)+
λ
rnd
(t)
При этом зависимость
λ
det
(t) оказывается кусочно-
непрерывной. Данная зависимость на временном
интервале [T
1
,T
3
] (T
3
=arg(max[
λ
(t)]) — момент времени,
в который данная зависимость достигает своего макси-
мального значения). При этом, если поместить начало
системы отсчета времени в момент начала футбольного
матча, то всегда T
3
< 0. Далее на временном интервале
[T
1
,T
3
] зависимость
λ
det
(t) уменьшается от максималь-
ного значения
λ
max
до 0. Таким образом, зависимость
λ
det
(t) оказывается зависящей от 3-х параметров:
λ
max
,
T
1
, T
2
, T
3
(рис. 3).
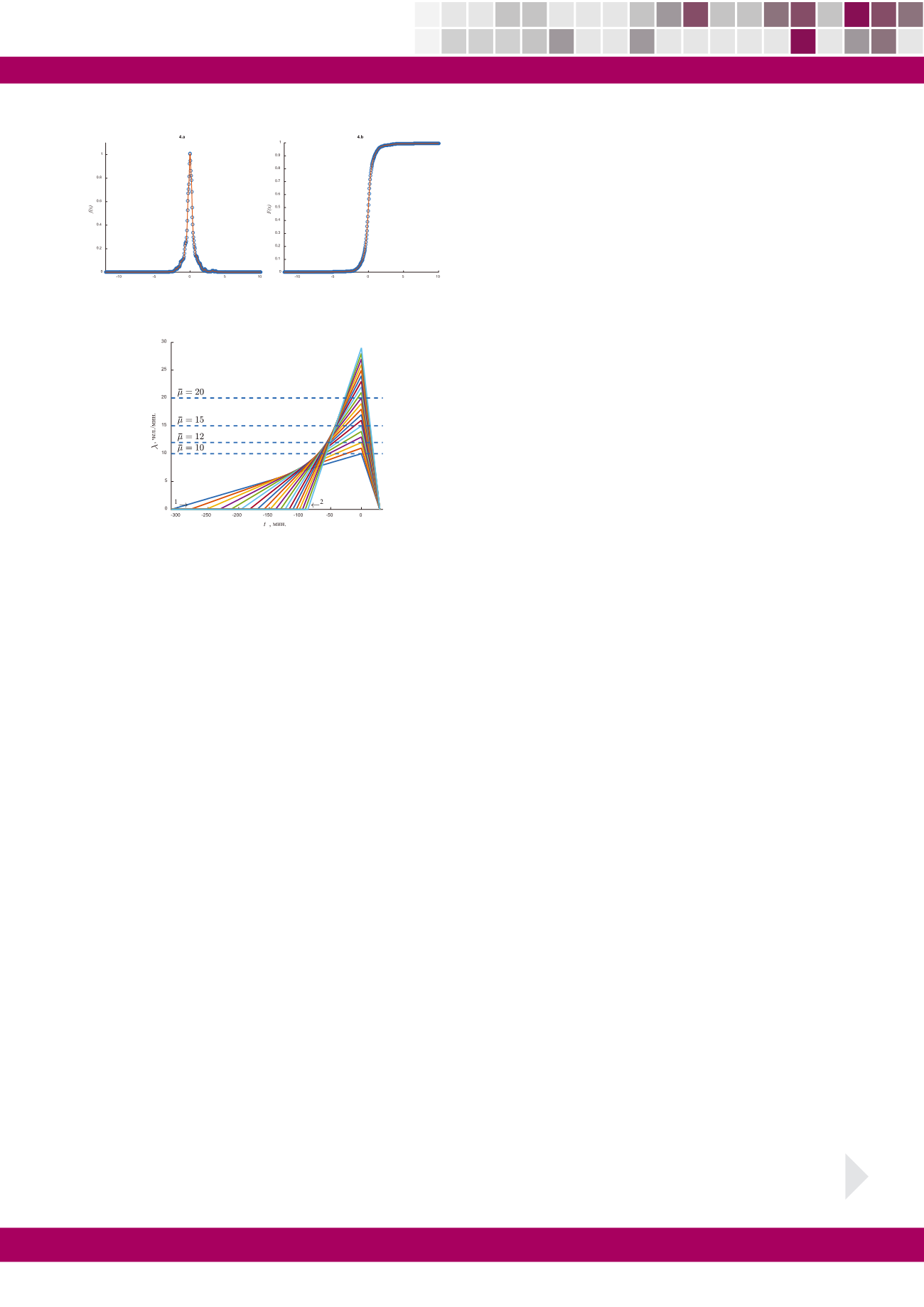
Типичные закон распределения и функция распре-
деления случайной составляющей
λ
rnd
(t) представлена
на рис. 2.
Из рис. 2 видно, что распределение внешне похоже
на нормальное, а дисперсия не очень большая.
Описание программной реализация имитационной
модели ИКПС, обеспечивающая учет обеих составляю-
щих зависимости
λ
(t), а также результаты, подтвержда-
ющие ее работоспособность, приведены в [3].
3. ОБОСНОВАНИЕ ВЫБОРА ПОКАЗАТЕЛЕЙ
СОСТОЯНИЯ ИКПС
Наличие программной реализации имитационной
модели ИКПС позволило провести систематические
исследования особенностей функционирования данной
системы при различных значениях параметров
λ
max
,
T
1
, T
2
, T
3
детерминированной составляющей
λ
det
(t)
и случайной составляющей
λ
rnd
(t). В том числе, были
вычислены зависимости: длины очереди посетителей
(в терминах СМО — длины очереди заявок) от времени:
L=L(t)
(2)
среднего время ожидания посетителя (в терминах
СМО — заявки) в очереди от времени:
τ
w
=
τ
w
(t)
(3)
числа вошедших на стадион посетителей от времени
(число обслуженных заявок в терминах СМО):
N=N(t)
(2)
примеры которых представлены на рис. 4.
Таким образом, анализ результатов моделирования
ИКПС, показал, что данную систему можно харак-
теризовать следующим набором макроскопических
показателей, которые представляют интерес не только
для конструкторов на этапе проектирования и модер-
низации ИКПС, но и служб безопасности объектов
проведения массовых мероприятий при проведении
массовых мероприятий:
1. Числом посетителей, вошедших к моменту начала
матча
N
0
;
2. Временем, необходимым для обслуживания всех
посетителей
T
ALL
;
3. Максимальным значением длины очереди
L
max
;
4. Максимальным значением длительности ожида-
ния в очереди
τ
w
max
;
5. Моментом времени, в который достигается макси-
мальная длина очереди
t
L
max
;
6. Моментом времени, в который достигается макси-
мальная длительность ожидания в очереди
t
τ
w max
,
которые, в свою очередь, оказываются завися-
щими от параметров
λ
max
, T
1
, T
2
, T
3
, μ и случайной
составляющей
λ
(t).
4. ВАРИАНТЫ ПРИМЕНЕНИЯ
Разработанная технология обеспечивает решение
широкого круга задач как на этапе проектирования
и модернизации ИКПС, так и на этапе их эксплуатации,
в том числе:
1.
При заданных значениях параметров
λ
max
, T
1
, T
2
, T
3
,
μ и случайной составляющей
λ
(t) вычислять: число
посетителей, вошедших к моменту начала матча
N
0
; время, необходимому для обслуживания всех
посетителей
T
ALL
; максимальное значение длины
очереди
L
max
; максимальное значение длительности
ожидания в очереди
τ
w
max
; момент времени, в кото-
рый достигается максимальная длина очереди
t
L
max
;
моментом времени, в который достигается макси-
мальная длительность ожидания в очереди
t
τ
w max
,.
2.
Для заданных значений параметров
λ
max
, T
1
, T
2
,
T
3
, случайной составляющей
λ
(t), максимального
значения длины очереди
L
max
; максимального
значения длительности ожидания в очереди
τ
w
max
определять количество турникетов ИКПС и их
интенсивность обслуживания посетителей μ.
3.
Для заданных значений параметров
λ
max
, T
2
, T
3
,
случайной составляющей
λ
(t), μ, максимального
значения длины очереди
L
max
; максимального
значения длительности ожидания в очереди
t
τ
w max
,
определять значение T
1
, такое, что к моменту нача-
Рисунок 2.
a.
Плотность распределения случайной составляющей
λ
rnd
(t)
b.
функция распределения случайной составляющей
λ
rnd
(t)
Рисунок 3.
Примеры зависимостей
λ
det
(t)
при различных значениях
параметров
λ
max
, T
1
, T
2
, T
3
39


